Adversarial Neural Cryptography in Theano
Last week I read Abadi and Andersen’s recent paper [1], Learning to Protect Communications with Adversarial Neural Cryptography. I thought the idea seemed pretty cool and that it wouldn’t be too tricky to implement, and would also serve as an ideal project to learn a bit more Theano. This post describes the paper, my implementation, and the results.
The setup
The authors set up their experiment as follows. We have three neural networks, named Alice, Bob, and Eve. Alice wishes to communicate an N bit message P to Bob. Alice and Bob also share a key (which you can think of as a password) of N bits.
Alice takes the message and the key, and encrypts the message, producing a communication C of N bits. Bob receives this communication, and then attempts to decrypt it, producing PBob.
Unfortunately for Bob and Alice, Eve intercepts Alice’s communication C. She then decrypts this message herself, producing her attempted recovery of P, which is called PEve.
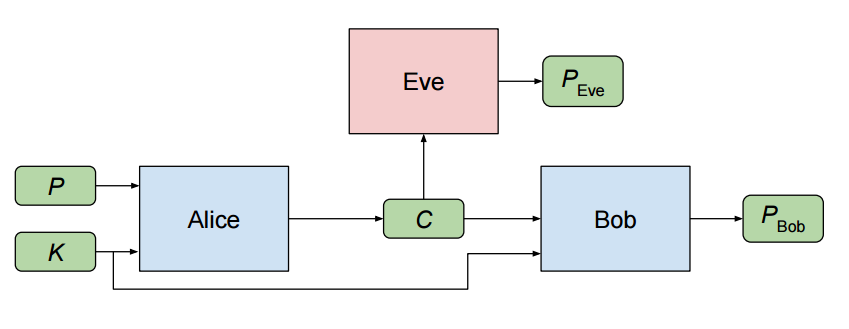 Figure 1: The adversarial network setup diagram given in [1].
Figure 1: The adversarial network setup diagram given in [1].
Neural networks
As mentioned, Alice, Bob and Eve are all neural networks. All three of these networks are quite similar.
Alice (Figure 2) takes as input the message and key vectors, concatenated into one long vector of length 2N. This then passes through a single fully-connected hidden layer of size 2N. It then passes through what I will refer to as the standard convolutional setup, which takes this 2N-length vector, passes it through a number of 1D convolution filters, and eventually outputs an N-length vector. This is the communication C that gets sent to Bob.
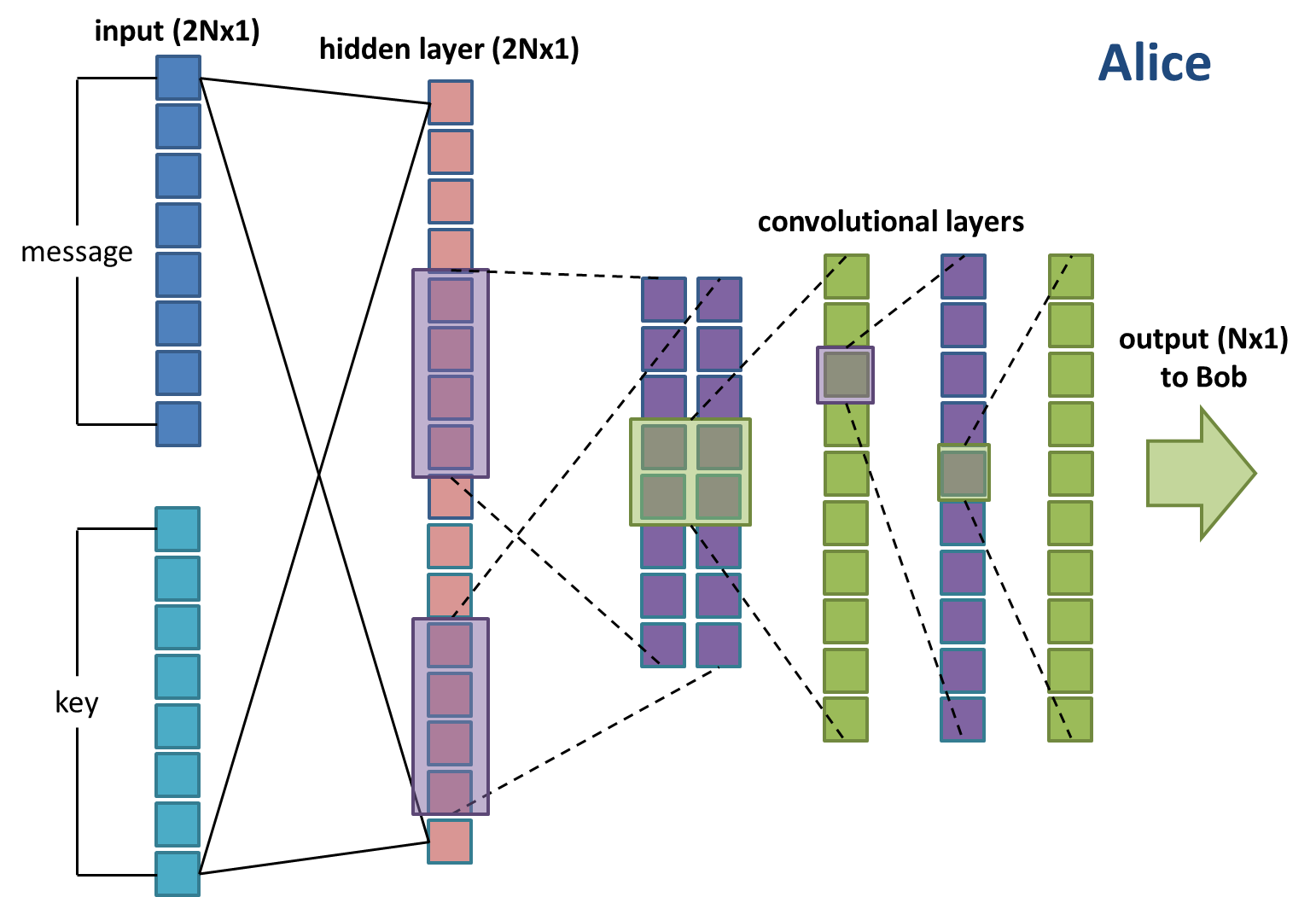
Figure 2: Alice’s neural network setup.
Bob’s network (Figure 3) is identical to Alice’s, except that his input is the concatenation of the communication and the key.
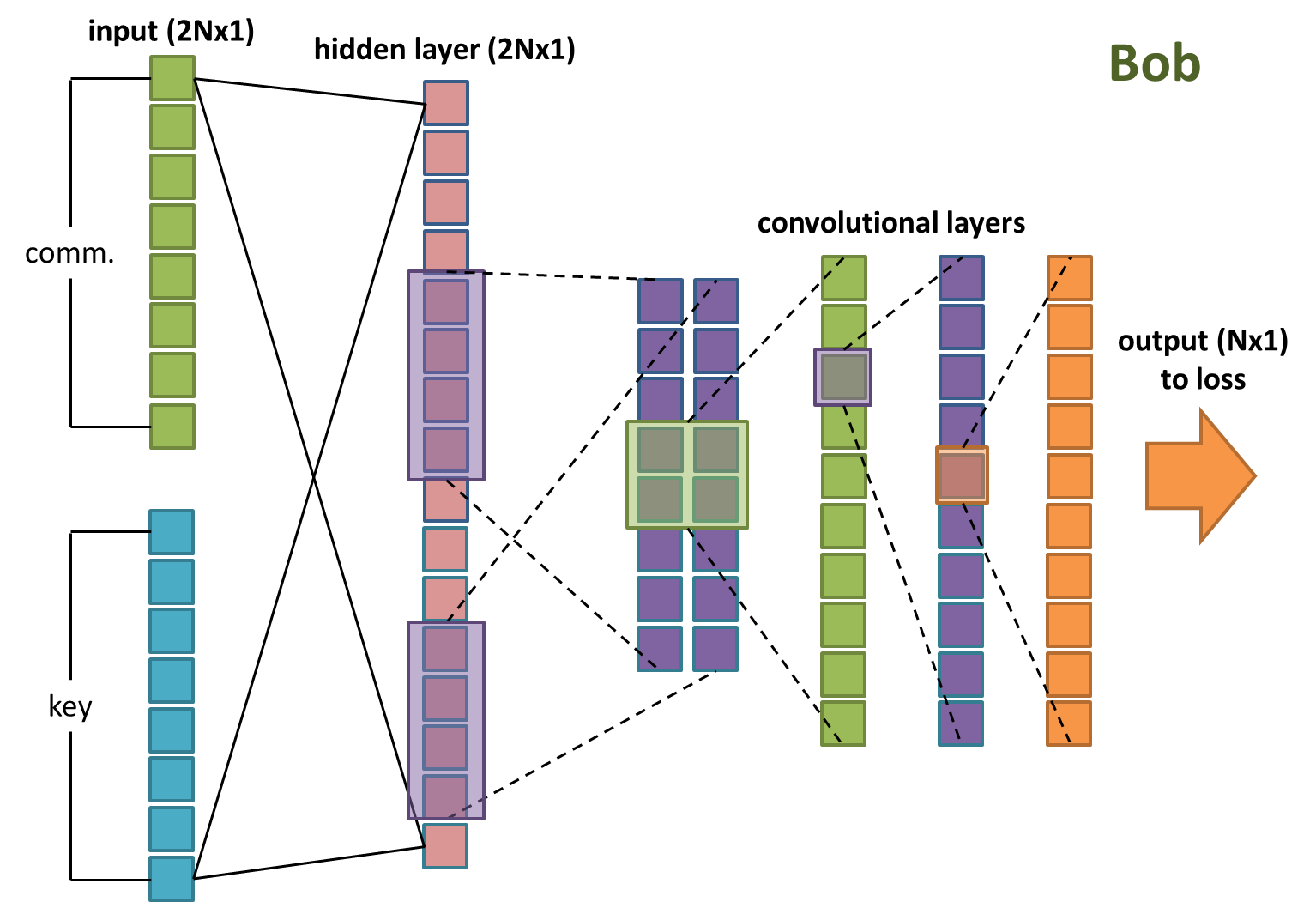
Figure 3: Bob’s neural network setup.
Eve’s network is also quite similar to Bob and Alice’s. However her input is just the communication C. She also has an additional fully-connected hidden layer of size 2N prior to the standard convolutional setup: the authors wanted to make Eve a bit more complex in order to give her a better chance of figuring out how to decrypt C.
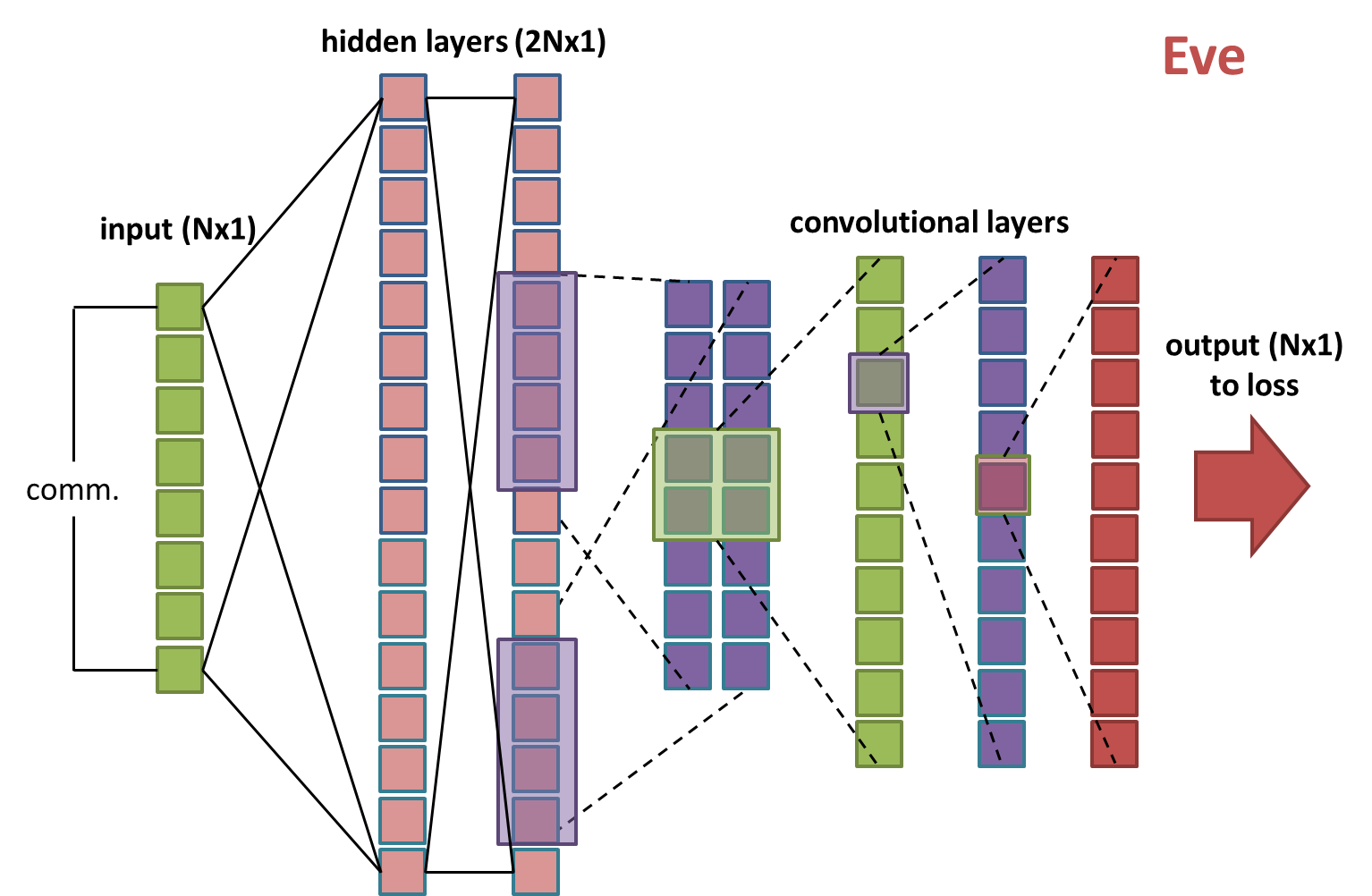
Figure 4: Eve’s neural network setup.
The following table gives the output dimensionality of each layer in each network:
| Layer | Output shape |
|---|---|
| Alice input | 2N |
| Alice hidden | 2N |
| Alice convolutional | (2, 2N+1) –> (4, N) –> (4, N) –> (1, N) |
| Bob input | 2N |
| Bob hidden | 2N |
| Bob convolutional | As per Alice |
| Eve hidden 1 | 2N |
| Eve hidden 2 | 2N |
| Eve convolutional | As per Alice |
Loss functions
The next ingredient are the loss functions:
Eve’s loss function is simply the absolute difference between the message vector P and her attempt at decrypting it PEve. This loss is backpropagated through the weights in the Eve network to update her weights.
LossEve = Eve L1 error = abs(P - PEve)
Bob and Alice’s loss function is also the absolute decryption error, plus an additional term that signifies how well Eve is currently decrypting the message. This additional term is:
(N / 2 - Eve L1 error)2 / (N / 2)2
This is minimised when Eve gets half the bits correct, on average, in her decryption, which indicates that she is doing no better than random guessing. The gradient of this loss function is used to update the weights in both the Bob and Alice networks. Putting these together, we have:
LossBob = Bob L1 error + (N / 2 - Eve L1 error)2 / (N / 2)
Adversarial training
Training then proceeds in an adversarial way: we train Bob and Alice for a while until they are communicating effectively, then we train Eve for some time, until she learns to decrypt the message. Then we train Bob and Alice again, who figure out how to fool Eve’s current decryption method. Then we train Eve again, who cracks the improved encryption, and so on. The authors find that after a while, Bob and Alice’s encryption becomes too strong for Eve to be able to learn to crack it.
Theano implementation
The implementation is fairly straightforward. I have used some custom classes, HiddenLayer() and ConvLayer() for adding standard NN layers. You can find these in the layers.py file.
We first need to define our batch size and N up front. I have added the possibility to have different lengths for the key, message and communication, however I have not tested this; changing it might cause issues.
batch_size = 512
msg_len = 16
key_len = 16
comm_len = 16Alice and Bob
For Alice and Bob we just create a fairly straightforward sequential NN:
# Tensor variables for the message and key
msg_in = T.matrix('msg_in')
key = T.matrix('key')
# Alice's input is the concatenation of the message and the key
alice_in = T.concatenate([msg_in, key], axis=1)
# Alice's hidden layer
alice_hid = HiddenLayer(alice_in,
input_size=msg_len + key_len,
hidden_size=msg_len + key_len,
name='alice_to_hid',
act_fn='relu')
# Reshape the output of Alice's hidden layer for convolution
alice_conv_in = alice_hid.output.reshape((batch_size, 1, msg_len + key_len, 1))
# Alice's convolutional layers
alice_conv = StandardConvSetup(alice_conv_in, 'alice')
# Get the output communication
alice_comm = alice_conv.output.reshape((batch_size, msg_len))
# Bob's input is the concatenation of Alice's communication and the key
bob_in = T.concatenate([alice_comm, key], axis=1)
# He decrypts using a hidden layer and a conv net as per Alice
bob_hid = HiddenLayer(bob_in,
input_size=comm_len + key_len,
hidden_size=comm_len + key_len,
name='bob_to_hid',
act_fn='relu')
bob_conv_in = bob_hid.output.reshape((batch_size, 1, comm_len + key_len, 1))
bob_conv = StandardConvSetup(bob_conv_in, 'bob')
bob_msg = bob_conv.output.reshape((batch_size, msg_len))Eve
Eve is similarly implemented. We just need to use alice_comm in her inputs.
# Eve see's Alice's communication to Bob, but not the key
# She gets an extra hidden layer to try and learn to decrypt the message
eve_hid1 = HiddenLayer(alice_comm,
input_size=comm_len,
hidden_size=comm_len + key_len,
name='eve_to_hid1',
act_fn='relu')
eve_hid2 = HiddenLayer(eve_hid1,
input_size=comm_len + key_len,
hidden_size=comm_len + key_len,
name='eve_to_hid2',
act_fn='relu')
eve_conv_in = eve_hid2.output.reshape((batch_size, 1, comm_len + key_len, 1))
eve_conv = StandardConvSetup(eve_conv_in, 'eve')
eve_msg = eve_conv.output.reshape((batch_size, msg_len))Loss functions
Here we just implement the loss equations described in the previous section. Note that the additional term in Bob’s loss function is a bit simpler than the equation described above. Things have been set up such that a mean error of 1 means that half the bits were correctly decrypted (as bits are input as either -1 or 1, so a single error = 2). Hence the N/2 terms can be dropped from the implementation.
# Eve's loss function is the L1 norm between true and recovered msg
decrypt_err_eve = T.mean(T.abs_(msg_in - eve_msg))
# Bob's loss function is the L1 norm between true and recovered
decrypt_err_bob = T.mean(T.abs_(msg_in - bob_msg))
# plus (N/2 - decrypt_err_eve) ** 2 / (N / 2) ** 2
# --> Bob wants Eve to do only as good as random guessing
loss_bob = decrypt_err_bob + (1. - decrypt_err_eve) ** 2.Training functions
The only tricky-ish thing here is making sure that the training function for Alice and Bob updates all their parameters, while Eve’s only updates her parameters. I use lasagne.adam for an implementation of the Adam SGD optimiser. I put the functions in dictionaries for ease of use in adversarial training.
# Get all the parameters for Bob and Alice, make updates, train and pred funcs
params = {'bob' : get_all_params([bob_conv, bob_hid,
alice_conv, alice_hid])}
updates = {'bob' : adam(loss_bob, params['bob'])}
err_fn = {'bob' : theano.function(inputs=[msg_in, key],
outputs=decrypt_err_bob)}
train_fn = {'bob' : theano.function(inputs=[msg_in, key],
outputs=loss_bob,
updates=updates['bob'])}
pred_fn = {'bob' : theano.function(inputs=[msg_in, key], outputs=bob_msg)}
# Get all the parameters for Eve, make updates, train and pred funcs
params['eve'] = get_all_params([eve_hid1, eve_hid2, eve_conv])
updates['eve'] = adam(decrypt_err_eve, params['eve'])
err_fn['eve'] = theano.function(inputs=[msg_in, key],
outputs=decrypt_err_eve)
train_fn['eve'] = theano.function(inputs=[msg_in, key],
outputs=decrypt_err_eve,
updates=updates['eve'])
pred_fn['eve'] = theano.function(inputs=[msg_in, key], outputs=eve_msg)Convolution layers
Since it is used in all three networks, I made a custom class for the standard convolutional setup. It stores all the parameters and tensors relavent to all of the convolutional layers in the model. I have tried to match the description of the convolution setup described in the paper:
class StandardConvSetup():
'''
Standard convolutional layers setup used by Alice, Bob and Eve.
Input should be 4d tensor of shape (batch_size, 1, msg_len + key_len, 1)
Output is 4d tensor of shape (batch_size, 1, msg_len, 1)
'''
def __init__(self, reshaped_input, name='unnamed'):
self.name = name
self.conv_layer1 = ConvLayer(reshaped_input,
filter_shape=(2, 1, 4, 1), #num outs, num ins, size
image_shape=(None, 1, None, 1),
stride=(1,1),
name=self.name + '_conv1',
border_mode=(2,0),
act_fn='relu')
self.conv_layer2 = ConvLayer(self.conv_layer1,
filter_shape=(4, 2, 2, 1),
image_shape=(None, 2, None, 1),
stride=(2,1),
name=self.name + '_conv2',
border_mode=(0,0),
act_fn='relu')
self.conv_layer3 = ConvLayer(self.conv_layer2,
filter_shape=(4, 4, 1, 1),
image_shape=(None, 4, None, 1),
stride=(1,1),
name=self.name + '_conv3',
border_mode=(0,0),
act_fn='relu')
self.conv_layer4 = ConvLayer(self.conv_layer3,
filter_shape=(1, 4, 1, 1),
image_shape=(None, 4, None, 1),
stride=(1,1),
name=self.name + '_conv4',
border_mode=(0,0),
act_fn='tanh')
self.output = self.conv_layer4.output
self.layers = [self.conv_layer1, self.conv_layer2,
self.conv_layer3, self.conv_layer4]
self.params = []
for l in self.layers:
self.params += l.paramsTraining
To perform the adversarial training, I made a train() function that would train either Alice and Bob or Eve for some time. We then just iterate between calling this function on Alice and Bob, and then for Eve. The gen_data() function generates batch_size random message and key pairs. We train according to the loss, but for plotting we just store the decryption error for the party that is currently being trained.
# Function for training either Bob+Alice or Eve for some time
def train(bob_or_eve, results, max_iters, print_every, es=0., es_limit=100):
count = 0
for i in range(max_iters):
# Generate some data
msg_in_val, key_val = gen_data()
# Train on this batch and get loss
loss = train_fn[bob_or_eve](msg_in_val, key_val)
# Store absolute decryption error of the model on this batch
results = np.hstack((results,
err_fn[bob_or_eve](msg_in_val, key_val).sum()))
# Print loss now and then
if i % print_every == 0:
print 'training loss:', loss
# Early stopping if we see a low-enough decryption error enough times
if es and loss < es:
count += 1
if count > es_limit:
break
return np.hstack((results, np.repeat(results[-1], max_iters - i - 1)))
# Initialise some empty results arrays
results_bob, results_eve = [], []
adversarial_iterations = 60
# Perform adversarial training
for i in range(adversarial_iterations):
n = 2000
print_every = 100
print 'training bob and alice, run:', i+1
results_bob = train('bob', results_bob, n, print_every, es=0.01)
print 'training eve, run:', i+1
results_eve = train('eve', results_eve, n, print_every, es=0.01)Results
I trained both Alice and Bob, and then Eve, for up to 2000 iterations at a time (early stopping occurred if the decryption error was below 0.01 for a while). I did 60 overall repetitions of this adversarial training setup. I then plotted the minimum decryption error achieved by Bob and by Eve in each of these 60 runs (Figure 5).
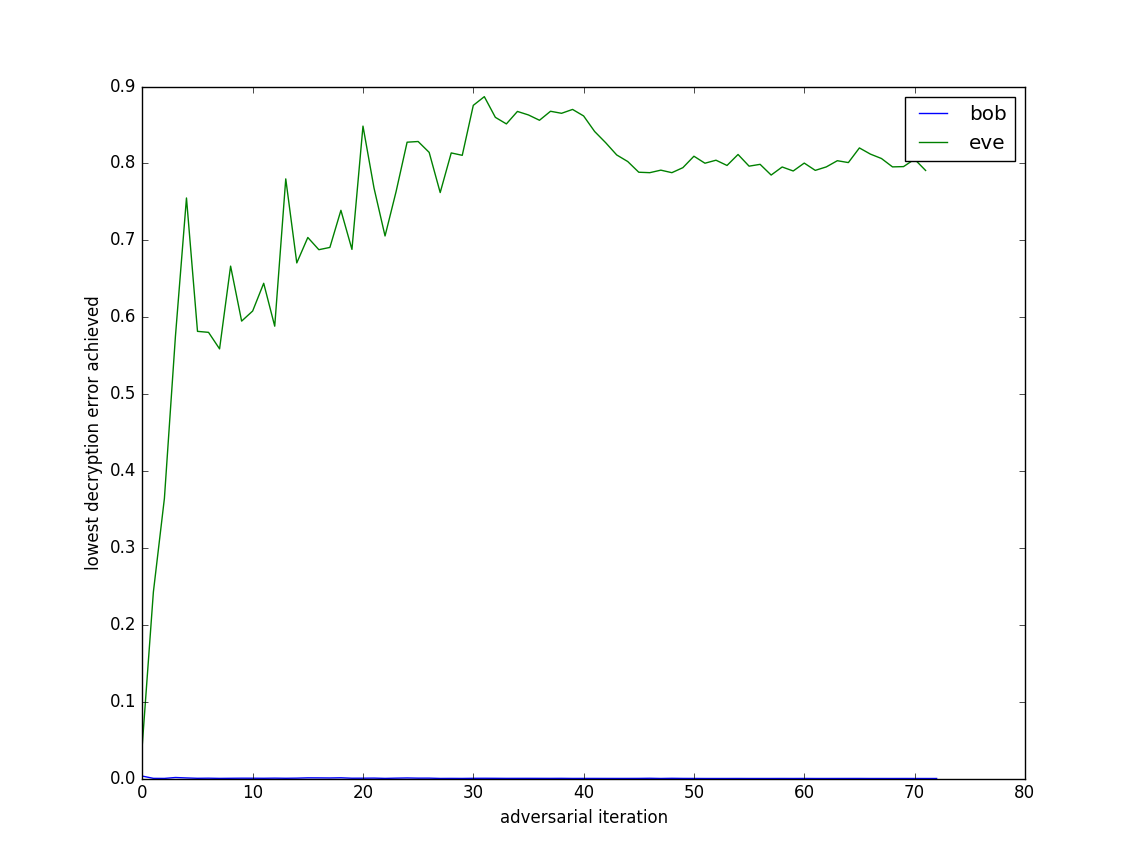 Figure 5: Bob and Eve’s decryption errors over 60 adversarial training iterations.
Figure 5: Bob and Eve’s decryption errors over 60 adversarial training iterations.
So, it seems to work. After a few adversarial rounds, Bob and Alice figure out a way to effectively scramble the communication such that Eve cannot learn how to decrypt it.
I also tested the setup without the four convolutional layers, instead replacing this with an additional 2N in, 1N out hidden layer (Figure 6).
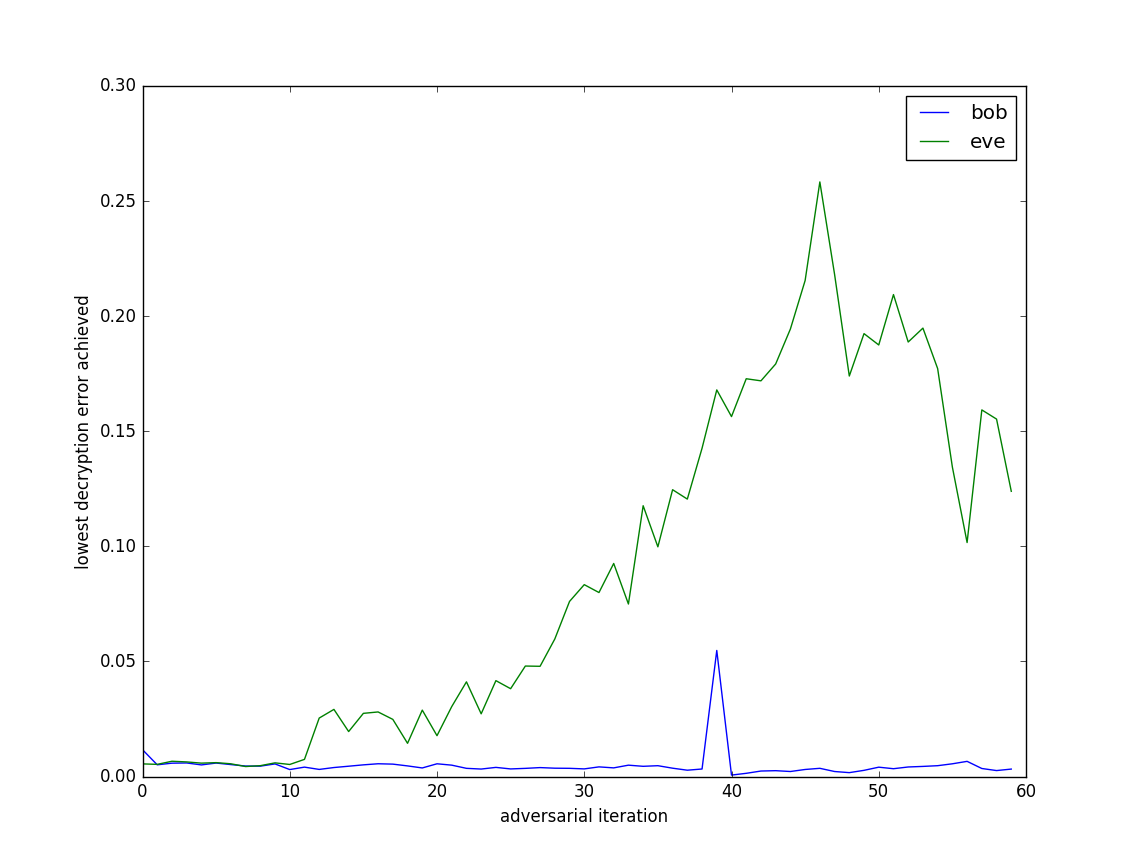 Figure 6: Bob and Eve’s decryption errors over 60 adversarial training iterations, with the convolutional phase of the network excluded.
Figure 6: Bob and Eve’s decryption errors over 60 adversarial training iterations, with the convolutional phase of the network excluded.
This seems to suggest that the convolution layers helps, but perhaps it is still possible to achieve the goals of this experiment without it - Eve still isn’t able to perfectly recover the message in this setup either.
Final thoughts
I should note that this paper didn’t receive much love when it was posted on the Reddit MachineLearning forum. And I have to say I kind of agree with the points made in that discussion: really the fact that this works doesn’t mean it has created good encryption. Rather it more just speaks to the weakness of the Eve network in its ability to decrypt the message. This is sort of reflected by the fact that this setup still seems to work without the convolution layers (Figure 6). Still, it is an interesting idea, and I don’t think I’m in a position to judge its academic merit.
Thanks for reading - thoughts, comments or questions are welcome!
References
1: Abadi, M & Andersen, D. Learning to Protect Communications with Adversarial Neural Cryptography. October 24 2016. Google Brain.
